scheme学习笔记

发表于 | |

学习scheme是为了学习了解函数式编程，目前看的是入门教材计算机程序的构造和解释(SICP)。

求值顺序

1
(define (square x) (* x x))

求值(square (+ 2 3))可能有2种求值方式:

1 正则序求值:先展开而后规约

1
2
3
=> (* (+ 2 3) (+ 2 3))
=> (+ (* 2 2) (* 2 3) (* 2 3) (* 3 3))
=> 25

2 应用序求值:先求值参数而后应用

1
2
3
=> (square 5)
=> (* 5 5)
=> 25

可以用下面的方法判断一个解释器采用的是正则序还是应用序的进行求值运算的。

1
2
3
4
5
6
7
8
9
10
11
;判断scheme(racket)
>> (define (test x) 1)
>> (test (/ 1 0))
=> /: division by zero
;说明racket是采用应用序求值
// 判断js(V8)
>> let test = x => 1;
>> test(1/0)
=> 1
// 说明v8解释采用的是正则序求值

lambda和let结构

1
2
3
4
5
(define (square x) (* x x))
(square 2) => 4
((lambda (x) (* x x)) 2) => 4
;lambda返回过程，而过程定义不返回这样就意味着lambda可以定义即调用
;类比js里立即函数调用

let则更近一步，将实参写入形参

1
2
3
4
5
6
7
8
9
(define x 1)
(define y 2)
(
  let (
    (x 3)
    (y 4)
  )(+ x y)
)
;7

可以类比js函数默认值,js提供改变形参的能力。说明此处let和js里let作用不一样！

1
2
3
4
let x = 1, y = 2;
let f = (x = 3, y = 4) => x + y;
f();      // 7
f(x, y);  // 3

拓展阅读:λ演算、各种组合子

let和let*、letrec

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#lang racket
(let ((x 2) (y 5))
  (let ((x 6) (z (+ x y)))
    (* z x)))
;;; => 42
(let ((x 2) (y 5))
  (let* ((x 6)(z (+ x y)))
    (* z x)))
;;; => 66
;;; letrec局部内递归，内部绑定互相引用
(letrec ((even?
          (lambda (x)
            (if (= x 0) #t
                (odd? (- x 1)))))
         (odd?
          (lambda (x)
            (if (= x 0) #f
                (even? (- x 1))))))
  (even? 88))

等价的js代码

1
2
3
4
5
6
7
((isEvn = x => x === 0
    ? true 
    : isOdd(x-1),
  isOdd = x => x === 0 
    ? false 
    : isEvn(x-1)
 ) => isEvn(88))()

模式匹配

提供比if,cond更好的代码分支结构

1
2
3
4
5
6
7
8
9
10
11
12
#lang racket
(define (type arg)
  (match arg
    [(? number? arg) "number"]
    [(? pair? arg) "pair"]
    [(? list? arg) "list"]
    ["+" "cal>+"]
    ["-" "cal>-"]
    ["*" "cal>*"]
    ["/" "/"]
    [(? string? arg) "string"]
    [(? arg) "other"]))

语法扩展define-syntax

例如定义一个while循环：

1
2
3
4
5
6
7
(define-syntax while
  (syntax-rules ()
    ([_ test body ...]
     (let loop ()
       (if test
         body ...
         (loop))))))

其它总结

语法方面:
->:类型转化，例如(string->number "1")
[]:等同于()但必须成对出现，主要让代码方便阅读，总比一大堆()看起来好看吧
?:类型判断，比如equal?,number?
'(a b c):list,相当于(list a b c)
当然我只看了前3章，有些东西也没细看。结合前几张内容总结一些知识点如下(目前有些东西不太理解，可能以后再看时稍微好理解一点):
高阶函数、闭包、模块化、并发控制、流(惰性求值)、元编程等、流程控制call/cc、Continuation/CPS

书上的一些小例子

1.牛顿法求平方根
求x的平方根y，假设一个y，然后求y和x/y的平均值以获得更好的逼近.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#lang racket
;计算平均值
(define (avg x y)
  (/ (+ x y) 2))
;绝对值
(define (abs x)
  (if (< x 0) (- x) x))
;平方
(define (square x) (* x x))
;逼近检测,绝对误差不超过0.0001即可
(define (good-enough x y)
  (if (< (abs (- (square x) y)) 0.0001) true
    false))
;迭代平方根
(define (sqrt-iter x s)
  (if (good-enough (avg s (/ x s)) x)
    (avg s (/ x s))
    (sqrt-iter x (avg s (/ x s)))
  ))
;求平方根
(define (sqrt x)
  (sqrt-iter x 1.0))
  
;test cases
(sqrt 2)
(sqrt 4)
(sqrt 7)

测试结果如下:
sqrt
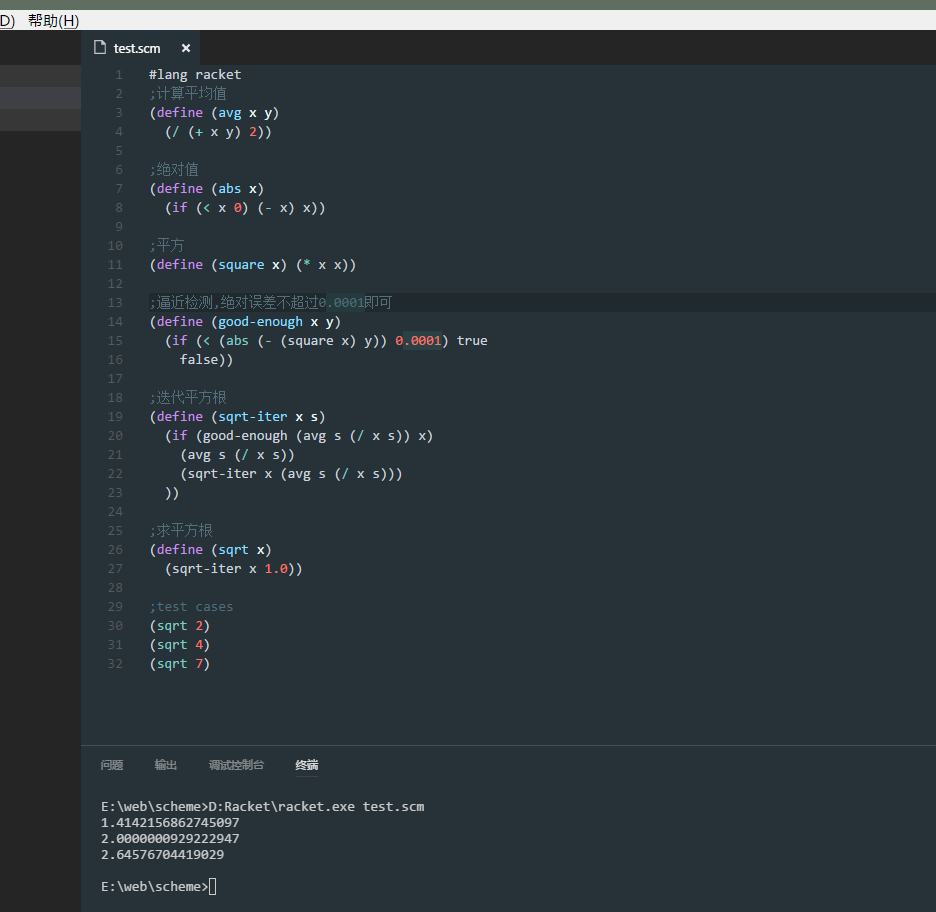
2.斐波那契数列
问题描述:斐波那契数列形如1 1 2 3 5 8 13 21 34 55 89 ...
当n = 0 或 n = 1时，F(n) = 1,当n > 1时, F(n) = F(n - 1) + F(n - 2)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#lang racket
;;;斐波那契数列的递归和尾递归实现
;递归
(define (fib n)
  (cond ((= n 0) 1)
        ((= n 1) 1)
        (else (+ 
                (fib (- n 1))
                (fib (- n 2))))))
;尾递归(迭代)
(define (fib2 a b n)
  (cond ((= n 0) a)
        ((= n 1) b)
        (else (fib2 b (+ a b) (- n 1)))))
;test cases
(fib 10)
(fib2 1 1 10)

3.一个计算最大公约数GCD的算法
欧几里得算法：令r = a % b，则a和b的公约数也正好是b和r的公约数。

1
2
3
4
5
6
7
8
9
10
11
#lang racket
;;;欧几里得求最大公约数算法
(define % remainder)    ;remainder是求余,为和其它语言看起来有相同形式
(define (gcd a b)
  (if (= b 0)
    a
    (gcd b (% a b))))
;test cases
(gcd 24 21)

4.函数组合compose实现
类似f(x)、g(x)、h(x)作用于同一个对象上r(x) = f(g(h(x)))

1
2
3
4
5
6
7
8
9
10
11
12
13
#lang racket
;;;fold-right实现类似于reduceRight
(define (fold-right op initial sequence)
  (if (null? sequence)
    initial
    (op (car sequence)
      (fold-right op initial (cdr sequence)))
  )
)
;实现一个compose函数复合
(define (compose . funcs)
  (lambda (x)
    (fold-right (lambda (f x) (f x)) x funcs)))

相对于javascript中,lodash的实现是while循环，相比较而言ramdba的实现更函数式，下面是一个仿照rambda实现pipe的一个示例

1
2
3
4
5
6
7
8
9
let compose = (...funcs) => (...args2) => funcs.reverse().reduce((prev, next) => {
  if (typeof prev === 'function') {
    prev = prev.apply(null, args2);
  }
  return next(prev);
}, x => x);
// test cases
compose(x => x * x, x => x + 1)(2);               // 9
compose(x => x / 8, x => x * x, x => x + 1)(3);   // 2

相应的fold-left，类似于reduce实现

1
2
3
4
5
6
7
8
#lang racket
(define (fold-left op initial seq)
  (define (iter result rest)
    (if (null? rest)
        result
        (iter (op result (car rest))
            (cdr rest))))
  (iter initial seq))

4.计算器

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#lang racket
(define calc
  (lambda (exp)
    (match exp
      [(? number? x) x]
      [`(,op ,e1 ,e2)
       (let ([v1 (calc e1)]
             [v2 (calc e2)])
       (match op
         ['+ (+ v1 v2)]
         ['- (- v1 v2)]
         ['* (* v1 v2)]
         ['/ (/ v1 v2)])
       )])))
;;; test cases
(calc '(+ 1 2))
(calc '(* (+ 1 2) (/ 8 2)))